¿QUÉ ES EL MOVIMIENTO?
●La
física Define al movimiento como el cambio deposición de un cuerpo con
respecto de un punto de referencia en el transcurso del tiempo.
● Esta definición sugiere que el movimiento contiene los siguientes elementos:
a) Punto de referencia:Es el lugar con respecto al cual se observa si el cuerpo se aleja o se acerca. EJEMPLO: cuando sales de tu casa para ir al colegio el punto de referencia es tu casa.
b) Distancia y desplazamiento: La distancia es la
medida del camino recorrido, es una magnitud
escalar.
EJEMPLO: Si una persona
dice camine 5 kilómetros Se comprende perfectamente. Pero
si esta misma persona dice salí de mi casa y camine 5
kilómetros hacia el Norte ya no se trata simplemente de
una distancia sino del desplazamiento que ha hecho
que es una magnitud vectorial porque tiene módulo
y dirección.

c) Rapidéz y velocidad: Si un automovilista dice voy a 50
km/h es la rapidez con la que se está desplazando y se
trata de una magnitud escalar pero sí dice voy a 50 km/h y
me dirijo hacia el colegio aparece además de la rapidez la
dirección, en ese caso se trata de la velocidad con la
que se dirige al colegio esta magnitud es un
vector porque tiene módulo y dirección. La
rapidez puede ser instantánea cuando se lo mide en un
instante dado como la que indica el velocímetro de un
automóvil también puede ser rapidez promedio cuando
se divide la distancia recorrida por un objeto
para el tiempo empleado en recorrerla esto es:
 Formula:
Formula:
rapidéz promedio= distancia/ tiempo recorrido; rapidez promedio= d/t.
 Ejemplo:
Ejemplo:
Si para recorrer de Quito a Cuenca, un bus se
ah tardado 10 horas, la rapidez promedio será:
442 km/10h= 44.2 km/h.
En resumen la distancia y la rapidez son magnitudes escalares, el desplazamiento y la velocidad Son magnitudes vectoriales.
CINEMATICA: CLASIFICACIÓN DE LOS MOVIMIENTOS.
Los movimientos pueden clasificarse según su trayectoria y según su velocidad.
Según la trayectoria el movimiento puede ser:
 Rectilineo: Cuando la trayectoria es una línea recta, es el caso de la pista de aterrizaje de los aviones.
Rectilineo: Cuando la trayectoria es una línea recta, es el caso de la pista de aterrizaje de los aviones.
 Curvilineo:
Cuando la trayectoria es una curva ,por ejemplo algunos tramos de las
carreras El camino de la Tierra alrededor del sol.
Curvilineo:
Cuando la trayectoria es una curva ,por ejemplo algunos tramos de las
carreras El camino de la Tierra alrededor del sol.
 Circular: Cuando la trayectoria es una circunferencia.
Circular: Cuando la trayectoria es una circunferencia.
Según la velocidad en movimiento puede ser:
 Uniforme: Cuando la velocidad permanece constante en el transcurso del tiempo.
Uniforme: Cuando la velocidad permanece constante en el transcurso del tiempo.
Ejemplo:
El sonido se transmite en el aire a una velocidad constante de 340 m/s.
 Variado: Cuando la velocidad varía con el tiempo.
Variado: Cuando la velocidad varía con el tiempo.
Ejemplo:
Si viajas en un automovil, observarás que la velocidad cambia frecuentemente.
 Uniformemente Variado: Cuando la velocidad aumenta o disminuye un valor constante cada unidad de tiempo.
Uniformemente Variado: Cuando la velocidad aumenta o disminuye un valor constante cada unidad de tiempo.
A esta variación constante se la denomina aceleración(a).
Ejemplo:
Al
caer un cuerpo libremente en el aire,sufre un incremento constante de
la velocidad de 9.8 m/s en cada segundo, esto es 9.8 m/s2.
*MOVIMIENTO RECTILINEO UNIFORME (MRU)
Un cuerpo se desplaza con movimiento rectilineo uniforme cuando su velocidad permanece consatnte en el transcurso del tiempo y su trayectoria va en linea recta. Tal es el caso de un ciclista que se desplaza en una pisat recta y plana, a una rapidez constante de 5m/s, durante 6s. Al final del primersegundo ha recorrido 5m, al final del segundo 10m, y asi sucesivamente.
Ejemplos:
1. La velocidad de la luz en el vacío es
c = 300 000 km/s. La luz del Sol tarda en llegar a la
Tierra 8 minutos y 19 segundos. Calcular la distancia entre el Sol y la Tierra.
La velocidad la hemos llamado c en vez de v ya que para la luz se
utiliza este nombre, pero el procedimiento es el mismo.
Por tanto, conocemos la velocidad, c, y el tiempo, t = 8 min 19s.
Podemos calcular la distancia:
Antes de sustituir tenemos que expresar el tiempo en una sola unidad.
Como la velocidad la tenemos en kilómetros por segundo,
pasamos el tiempo a segundos:
Por un lado, los 8 minutos son
Por tanto, el tiempo es
Ahora sustituimos los datos en la ecuación:
Por tanto, la distancia del Sol a la Tierra es de 149 700 000km, es decir,
casi 150 millones de kilómetros.
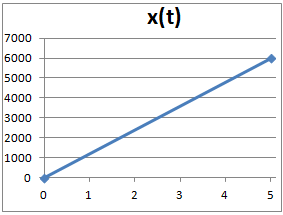
2.Dibujar la gráfica del espacio recorrido en función del tiempo y la
gráfica de la velocidad en función del tiempo del movimiento
rectilíneo uniforme de una aeronave que vuela a 1200 km/h.
La ecuación del movimiento rectilíneo uniforme es
Sustituimos la velocidad y obtenemos
Como la velocidad está en kilómetros por hora, la unidad de medida del
tiempo, t, será horas y la del espacio, x, en kilómetros.
Para dibujar la gráfica del espacio recorrido en función del tiempo,
damos dos valores a t y dibujamos el par (x,t).
Escogemos, por ejemplo,
Una vez dibujados los puntos
Sólo tenemos que unirlos en línea recta ya que sabemos que en este tipo
de movimiento el espacio es una recta con pendiente
la velocidad (la ecuación es una ecuación lineal):
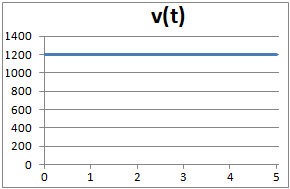
Como la velocidad es constante,
la gráfica de v(t) será una recta horizontal, una recta paralela al eje
de abscisas:
https://www.fisicalab.com/ejercicio/911#contenidos
MOVIMIENTO RECTILINEO UNIFORMEMENTE ACELERADO,SIN VELOCIDAD INCIAL.
Se denomina así a aquel movimiento rectilíneo que se caracteriza porque
su aceleración a permanece constante en el tiempo (en módulo y
dirección). En este tipo de movimiento el valor de la velocidad aumenta o
disminuye uniformemente al transcurrir el tiempo, esto quiere decir que
los cambios de velocidad son proporcionales al tiempo transcurrido, o,
lo que es equivalente, en tiempos iguales la velocidad del móvil aumenta
o disminuye en una misma cantidad.
Si se deja rodar una bola en un plano inclinado, esta arranca del resposo y su velocidad se va incrementando en el transcurso del tiempo de una manera constante, en cada segundo.
Este movimiento de la bola, es un movimiento uniformemente variado sin velocidad inicial, poque la velocidad inical (v) es cero 0, y a partir de este punto la velocidad tiene una aceleracion constante.
La velocidad que tiene la bola al fin de cada segundo es la velocidad final (Vf).
La direccion del desplazamiento va en linea recta.
Formulas :
Ejemplos:
1.- Un cuerpo se mueve, partiendo del re poso, con una aceleración constante de 8
m/s2. Calcular: a) la velocidad que tiene al cabo de 5 s, b) la distancia recorrida, desde el reposo, en los primeros 5 s.
Datos:
vi = 0 (m/s)
a = 8 (m/s2)
vf= vi+ at = 0 (m/s) + 8 (m/s2) x 5 (s) = 40 (m/s)
d = vi
t + at2/2 = 0 (m/s) x 5 (s) + 8 (m/s2) x (5 (s))2/ 2 = 100 (m)
2.- La velocidad de un vehículo aumenta uniformemente desde 15 km/h hasta 60
km/h
en 20 s. Calcular a) la velocidad media en km/h y en m/s, b) la
aceleración, c) la distancia, en metros, recorrida durante este tiempo.
Recuerde que para transformar de km/h a m/s hay que dividir por 3,6.
Datos:
vi= 15 (km/h) = 4,167 (m/s)
vf = 60 (km/h) = 16,67 (m/s)
t = 20 (s)
a = (vf– vi)/t = (16,67 (m/s) - 4,167 (m/s))/20 (s) = 0,625 (m/s2)
d = v
it + at
2/2 = 4,167 (m/s) x 20 (s) + 0,625 (m/s2) x (20 (s))
2/2 = 208,34 (m).
Movimiento Rectilíneo Uniformemente Variado (MRUV)
Se denomina así a aquel movimiento rectilíneo que se caracteriza
porque su aceleración a permanece constante en el tiempo (en módulo y
dirección). En este tipo de movimiento el valor de la velocidad aumenta o
disminuye uniformemente al transcurrir el tiempo, esto quiere decir que
los cambios de velocidad son proporcionales al tiempo transcurrido, o,
lo que es equivalente, en tiempos iguales la velocidad del móvil aumenta
o disminuye en una misma cantidad.
Veamos un ejemplo:
En este caso tenemos un móvil que se mueve horizontalmente
describiendo un MRUV en donde en cada segundo el valor de su velocidad
aumenta en 2 m/s. Debido a esto, el valor de la aceleración constante
con que se mueve el móvil es 2 metros por segundo cuadrado:
a = 2 m/s2.
MOVIMIENTO CURVILINEO.
Supongamos que el movimiento tiene lugar en el plano XY. Situamos un
origen y unos ejes y representamos la trayectoria del móvil, es decir, el conjunto de
puntos por los que pasa el móvil. Las magnitudes que describen un movimiento curvilíneo son:
Vector posición.
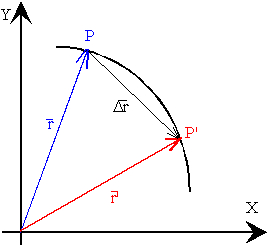
Como la posición del móvil cambia con el tiempo. En el instante
t, el móvil se encuentra en el punto P, o en otras palabras, su vector posición es
r y en el instante
t' se encuentra en el punto P', su posición viene dada por el
vector
r'.
Diremos que el móvil se ha desplazado
Δr=r’-r en el intervalo de tiempo
Δt=t'-t.
Dicho vector tiene la dirección de la secante que une los puntos P y P'.
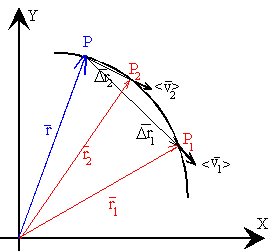
El vector velocidad media, se define como el cociente entre el vector
desplazamiento
Δr y el tiempo que ha empleado en
desplazarse
Δt.
<v>=r'−rt'−t=ΔrΔt
El vector velocidad media tiene la misma dirección que el vector desplazamiento, la
secante que une los puntos P y P
1 cuando se calcula la
velocidad media <
v1> entre los instantes
t y
t1.
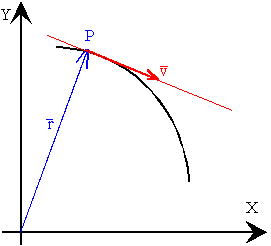
El vector velocidad en un instante, es el límite del vector velocidad
media cuando el intervalo de tiempo tiende a cero.
v=limΔ t→0ΔrΔt=drdt
Como podemos ver en la figura, a medida que hacemos tender el intervalo de tiempo a
cero, la dirección del vector velocidad media, la recta secante que une sucesivamente los
puntos P, con los puntos P
1, P
2....., tiende hacia la tangente a la
trayectoria en el punto P.
En el instante
t, el móvil se encuentra en P y tiene una velocidad
v cuya dirección es tangente a la trayectoria en dicho punto.
Vector aceleración
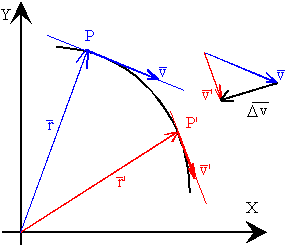
En el instante
t el móvil se encuentra en P y tiene una velocidad
v cuya dirección es tangente a la trayectoria en dicho punto.
En el instante
t' el móvil se encuentra en el punto P' y tiene una velocidad
v'.
El móvil ha cambiado, en general, su velocidad tanto en módulo como en dirección, en
la cantidad dada por el vector diferencia
Δv=v’-v.
Se define la aceleración media como el cociente entre el vector cambio de velocidad
Δv y el intervalo de tiempo
Δt=t'-t, en el que tiene
lugar dicho cambio.
<a>=v'−vt'−t=ΔvΔt
Y la aceleración
a en un instante
a=limΔ t→0ΔvΔt=dvdt
Resumiendo, las ecuaciones del movimiento curvilíneo en el plano XY son
x=x(t) vx=dxdt ax=dvxdty=y(t) vy=dydt ay=dvydt
La primera fila corresponde, a las ecuaciones de un movimiento rectilíneo a lo largo
del eje X, la segunda fila corresponde, a las ecuaciones de un movimiento rectilíneo a lo
largo del eje Y, y lo mismo podemos decir respecto del eje Z.
Por tanto, podemos considerar un movimiento curvilíneo como la composición de
movimientos rectilíneos a lo largo de los ejes coordenados.
Ejemplo 1:
Un automóvil describe una curva plana tal que sus
coordenadas rectangulares, en función del tiempo están dadas por las
expresiones:
x=2
t3-3
t2,
y=
t2-2
t+1
m. Calcular:
- Las
componentes de la velocidad en cualquier instante.
vx=dx/dt=6t2-6t
m/s
vy=dy/dt=2t-2
m/s
- Las
componentes de la aceleración en cualquier instante.
ax=
dvx/dt=12
t-6 m/s
2
ay=
dvy/dt=2 m/s
2
POSICIÓN
En
física, la posición de una partícula indica su localización en el
espacio o en el espacio-tiempo. Se representa mediante sistemas de
coordenadas.
En
mecánica clásica, la posición de una
partícula en el espacio se representa como una
magnitud vectorial respecto a un sistema de coordenadas de referencia. En
relatividad general,
la posición no es representable mediante un vector euclidiano, ya que
en el espacio-tiempo es curvo en esa teoría, por lo que la posición
necesariamente debe representarse mediante un conjunto de coordenadas
curvilíneas arbitrarias, que en general no pueden ser interpretadas como
las componentes de un
vector físico genuino. En
mecánica cuántica, la representación de la posición de una partícula es aún más compleja, debido a los efectos de
no localidad relacionados con el
problema de la medida de la mecánica cuántica.
En general, en un
sistema físico o de otro tipo, se utiliza el término posición para referirse al
estado físico o situación distinguible que exhibe el sistema. Así es común hablar de la posición del sistema en un diagrama que ilustre
variables de estado del sistema.
Vector posición en mecánica clásica
En
mecánica clásica, debido al carácter
euclídeo del espacio, la posición de una partícula se representa mediante el
vector de posición o
radio vector, usualmente simbolizado con la letra

o mediante las
coordenadas del punto geométrico del espacio en el que se encuentra la partícula.
La diferencia del vector posición entre dos posiciones distintas recibe el nombre de vector desplazamiento y se le designa por

(desplazamiento finito) o por

(desplazamiento infinitesimal)
SISTEMAS DE REFERENCIA
Podemos representar la posición de una partícula o de un punto del
espacio, respecto de un sistema de ejes, mediante las coordenadas
cartesianas (
x,
y,
z) del punto, o mediante el
vector de posición
de dicho punto respecto al origen "O" del sistema de coordenadas
(Figura 1). Dicho vector de posición se define como el vector que tiene
como origen el punto "O" y como extremo el punto "P", es decir, el
vector aplicado en el punto "O" que tiene como componentes las
coordenadas cartesianas x,
y,
z, del punto "P". Escribiremos

siendo

los
versores asociados a los ejes coordenados respectivos. En general, un sistema de referencia queda definido por un origen y una
base vectorial asociada. Si la base vectorial es
ortogonal (i.e., si los tres versores que la definen son perpendiculares entre sí), el sistema de referencia también es ortogonal.
TRASLACION Y ROTACION DEL SISTEMA
Merece particular atención considerar el vector de posición cuando cambia por traslación el
sistema de referencia,
pues entonces cambia el vector de posición del punto P. Entre los
vectores de posición del punto P respecto a los sistemas de referencia
de origen en O y en O′ existe la relación

y, consecuentemente, las componentes del vector de posición no son invariantes en las traslaciones del sistema de referencia.
De mismo modo, las componentes del vector de posición no son
invariantes en las rotaciones del sistema de referencia, transformando
sus componentes mediante la correspondiente
matriz de rotación.
Derivada temporal del vector de posición
Cuando la partícula permanece en reposo en el sistema de referencia,
sus coordenadas no cambian en el transcurso del tiempo y su vector de
posición será constante:

Si la posición de una partícula puntual
P cambia con el tiempo, en un instante dado se representa por:

En un sistema de referencia fijo, la base coordenada para expresar la
posición de vectores tiene la propiedad de permanecer fija, con lo cual
el vector velocidad respecto a un sistema inercial puede obtenerse
simplemente derivando las componentes del vector de posición respecto al
tiempo:

Esto contrasta con el caso de un sistema de referencia móvil, en los
que aparecen términos adicionales asociados al movimiento del
referencial.
Derivada del vector de posición en referenciales en rotación
Cuando el movimiento de la partícula se describe a un sistema de
referencia móvil (x,y,z) en rotación con respecto de un referencial fijo (X,Y,Z) con el que comparte el mismo origen, el vector de posición será el mismo en ambos referenciales y vendrá expresado por:

en el referencial móvil (
x,y,z). Puesto que los
versores cartesianos (i,j,k)son función del tiempo, al derivar el vector posición con respecto al tiempo aparecerán términos relacionados se obtiene:

siendo

la
velocidad angular asociada a la rotación del referencial móvil con respecto al referencial fijo.
En términos de la
geometría diferencial los términos adicionales tienen que ver con la conexión asociada al sistema de coordenadas o referencia escogido:

Donde:
 son los símbolos de Christoffel que caracterizan la conexión.
son los símbolos de Christoffel que caracterizan la conexión. son las componentes de la velocidad.
son las componentes de la velocidad.
Posición en mecánica relativista
En la teoría especial de la relatividad el espacio-tiempo de Minkowski tiene geometría pseudoeuclídea pero en lo esencial existe una biyección entre ese espacio y  por lo que puede definirse un cuadrivector posición análogo en muchos aspectos al vector posición de la mecánica clásica:
por lo que puede definirse un cuadrivector posición análogo en muchos aspectos al vector posición de la mecánica clásica:

La derivada de este vector respecto al tiempo propio resulta ser la cuadrivelocidad que es el análogo relativista de la velocidad de la mecánica clásica:

Sin embargo en la teoría general de la relatividad las cosas se complican debido a que en ese contexto el espacio-tiempo generalmente es curvo.
En ese caso no existe una biyección directa entre el espacio-tiempo y
el espacio euclídeo tridimensional y por tanto no resulta posible
describir la posición de un punto del espacio-tiempo mediante un vector
euclídeo. Aunque como el espacio-tiempo cuatridimensional es localmente difeomórfico con el espacio eclídeo tridimensional, pueden emplearse coordenadas curvilíneas
que tienen leyes de transformación tensorial similares a un
cuadrivector, aunque las cuatro coordenadas de un punto no pueden ser
identificadas con un cuadrivector.
Posición en mecánica cuántica
En mecánica cuántica no-relativista para la mayoría de los sistemas
no puede hablarse de la posición de una determinada partícula o incluso
de su trayectoria. Esto es una consecuencia del principio de incertidumbre de Heisenberg. En esta teoría las coordenadas intervienen sólo como argumento de la función de onda que describe un sistema, pero en general esas coordenadas no designan la posición de ninguna partícula.
DESPLAZAMIENTO
Moverse es desplazarse y desplazarse es cambiar de posición. Una manera de darse cuenta del movimiento de un cuerpo es a través del cambio de posición. Si un cuerpo material cambia su posición con respecto a otro escogido como referencia, se puede afirmar que ese cuerpo se ha desplazado.
Hoy día se sabe que el polo Norte celeste, partme de la bóveda celeste que está encima del polo norte se mueve en un pequeño círculo y vuelve a su posición original cada 26.000 años, de igual manera observando las estrellas, justo antes del amanecer y justo antes de la puesta del Sol se puede ver que éste cambia lentamente su posición respecto a las estrellas cada día, volviendo a su punto de partida después de 365 días y cuarto.
Una manera de darse cuenta del movimiento de un cuerpo es a través del cambio de su posición con respecto a otro cuerpo tomado como referencia. Si se observa algún cambio se dice que el cuerpo se ha desplazado.
Movimiento de nutación del eje de rotación terrestre
Los movimientos de las estrellas, del Sol y de los planetas (vínculo con la Historia) han sido detectados observando los cambios de posición de estos objetos en el cielo durante períodos relativamente largos de tiempo, la observación de estos desplazamientos ha permitido al hombre diferenciar estrellas de planetas, determinar planetas en otras estrellas, separar galaxias de otros astros, estudiar la influencia del movimiento del Sol sobre el clima de nuestro planeta y otros fenómenos importantes que tienen que ver con el movimiento de la Tierra en el cielo, ampliando así el conocimiento sobre el Universo donde él habita.
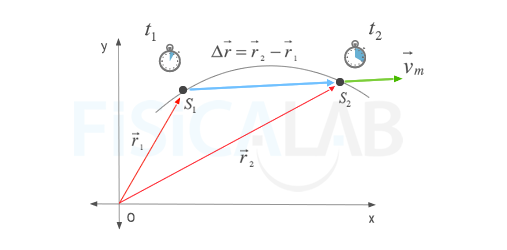 Velocidad MediaLa velocidad media de un cuerpo (verde) es un vector que tiene la misma dirección y sentido que el vector desplazamiento (azul) y cuyo módulo es el cociente entre el módulo de dicho vector y el tiempo transcurrido.
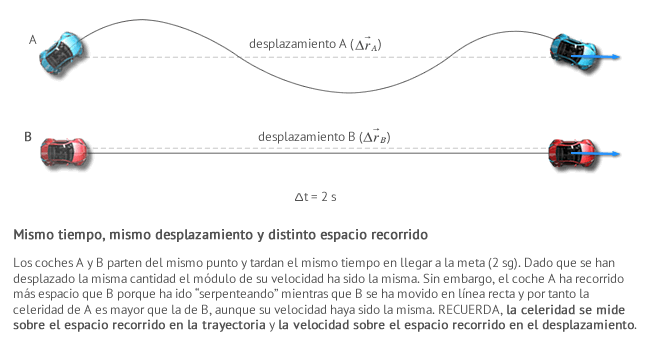
Velocidad MediaLa velocidad media de un cuerpo (verde) es un vector que tiene la misma dirección y sentido que el vector desplazamiento (azul) y cuyo módulo es el cociente entre el módulo de dicho vector y el tiempo transcurrido.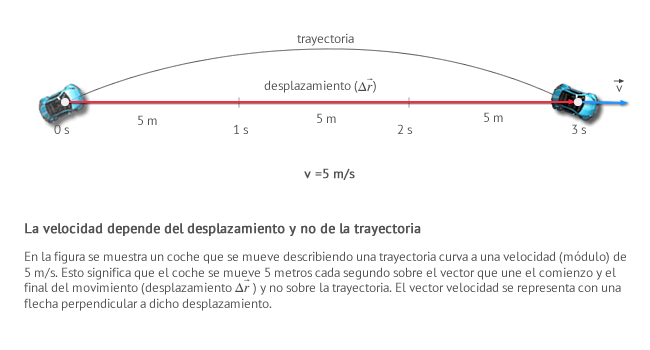
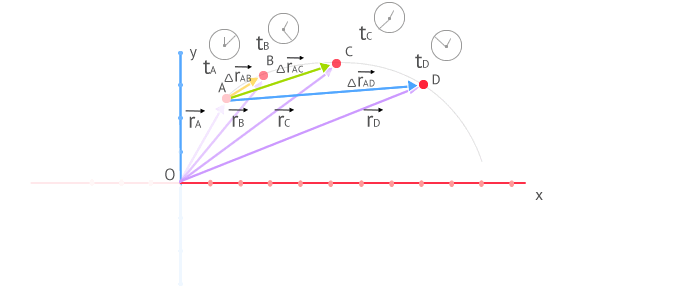



 Formula:
Formula: Rectilineo
Rectilineo







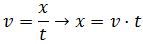
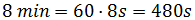
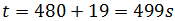
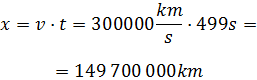
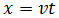
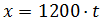
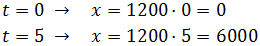
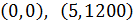




 Como la posición del móvil cambia con el tiempo. En el instante t, el móvil se encuentra en el punto P, o en otras palabras, su vector posición es r y en el instante t' se encuentra en el punto P', su posición viene dada por el
vector r'.
Como la posición del móvil cambia con el tiempo. En el instante t, el móvil se encuentra en el punto P, o en otras palabras, su vector posición es r y en el instante t' se encuentra en el punto P', su posición viene dada por el
vector r'.  El vector velocidad media, se define como el cociente entre el vector
desplazamiento Δr y el tiempo que ha empleado en
desplazarse Δt.
El vector velocidad media, se define como el cociente entre el vector
desplazamiento Δr y el tiempo que ha empleado en
desplazarse Δt.  El vector velocidad en un instante, es el límite del vector velocidad
media cuando el intervalo de tiempo tiende a cero.
El vector velocidad en un instante, es el límite del vector velocidad
media cuando el intervalo de tiempo tiende a cero.  En el instante t el móvil se encuentra en P y tiene una velocidad v cuya dirección es tangente a la trayectoria en dicho punto.
En el instante t el móvil se encuentra en P y tiene una velocidad v cuya dirección es tangente a la trayectoria en dicho punto.  o mediante las
o mediante las  (desplazamiento finito) o por
(desplazamiento finito) o por  (desplazamiento infinitesimal)
(desplazamiento infinitesimal)
 los
los 






 la
la 
 son los
son los  son las componentes de la velocidad.
son las componentes de la velocidad. por lo que puede definirse un cuadrivector posición análogo en muchos aspectos al
por lo que puede definirse un cuadrivector posición análogo en muchos aspectos al 

